Why am I getting dups with random.shuffle in Python? -

-

For a list of 10 ints, there are 10! Why possible order or permutation is random after only 5000 attempts? Does Schlämt duplicate? 

  & gt; & Gt; & Gt; L = class (10) & gt; & Gt; & Gt; RL = list ()> & Gt; & Gt; In the I category (5000): ... random. Shuffle (L) ... RL.Append (L [:]) ... & gt; & Gt; & Gt; RL = [tl (e)]> gt; & Gt; & Gt; Lane (Set (RL)) 4997 & gt; & Gt; & Gt; I, for EN enumerate (RL) t: ... if RL Cotet (T)> 1: ... printed, t ... 102 (7, 5, 2, 4, 0, 6, 9, 3, 1, 8) 258 (1, 4, 0, 2, 7, 3, 5, 9, 6, 8) 892 (1, 4, 0, 2, 7, 3, 5, 9, 6, 8) 2878 (7, 5, 2, 4, 0, 6, 9, 3, 1, 8) 4123 (5, 8, 0, 1, 7, 3, 2, 4, 6, 9) 4633 (5, 8, 0, 1, 7, 3, 2, 4, 6, 9) & gt; & Gt; & Gt; 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 3628800 & gt; & Gt; & Gt; 2 ** 19937 - 1 431542479738816264805523551633791983905393 [snip]> gt; & Gt; L = list ()> & Gt; & Gt; In the I category (5000): ... el.appand (random.choice (xrange (3628800)) ... & gt; & Gt; & Gt; Lane (Set (L)) 4997

EDIT: FWI, if there is a possibility of not having two for a single pair: p = (10! - 1) / 10! And the number of coincidences is: C = 5000! / 49 9 8! * 2! = 5000 * 4999/2 is likely to be a duplicate: 

  gt; & Gt; Import Mathematics & gt; & Gt; & Gt; F = math.factorial (10) & gt; & Gt; & Gt; P = 1.0 * (F -1) / F> & Gt; & Gt; C = 5000.0 * 4999/2> gt; & Gt; 1 - P ** C 0.96806256495611798

It is called.

According to this formula Wikipedia:

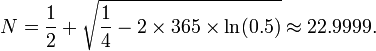
but with 365 with 10! To change you only need 2200 instances, so that there is a 50% chance of collision, and you are above top.


Comments

Post a Comment

Popular posts from this blog

oracle - The fastest way to check if some records in a database table? -

-
I have a big table to work with. I have to see that there are some records whose parent_id is equal to my passing value. Currently I do this by implementing "my_table using select count (*) where parent_id =: id"; If the result> 0, it means that they exist. Because this is a very large table, and I do not care what the actual number of records present, I just want to know if it exists, so I think count (*) Bit is disabled. How do I apply this requirement most quickly? I'm using Oracle 10. # Tips for Hibernation & amp; Tricks It suggests writing in such a way: Integer number = (integer) session .createQuery ("Select Count (*) to ...."). UniqueResult (); I do not know what is the magic of the unique rule? Why does it fast? To compare, select "1 from mytable where parent_id = passId and rowrum", which is more efficient? If you are not interested in the number of records, then there is an EXISTS query one: Select 'y'
Read more

php - multilevel menu with multilevel array -

-
Just ask someone to solve this problem? I want to create a multilevel menu I can not find the right solution generated with multilevel array, it always gets an array_push error My study came from the original idea But still my Can not match the need. This is my MySQL [code] ----- --------------------- --------------- | ID | PARENT_ID | Name | Link | Seq | 1 | 0 | Dashboad | Dashboard / | 1 | 2 | 0 | Menu 1 | Menu 1 / | 2 | 3 | 0 | Menu 2 | Menu 2 / | 3 | 4 | 0 | Menu 3 | Menu 3 / | 4 | 5 | 2 | Joint Add / | 1 | 6 | 3 | Joint Add / | 1 | 7 | 2 | Edit | Edit / | 2 | 8 | 4 | Joint Add / | 1 ------------------------------------------ [/ Code] I want to do something like this in my array array ('dashboard' = & gt; array ('id' = & gt; '' 'Dame' = & gt; 'Dashboard', 'Title' = & gt; 'Dashboard', 'MatchMin' = & gt; Base_URL (). 'Dashboard /', 'Active' => = & Gt; NULL), &
Read more

jQuery UI: Datepicker month format -

-
I am trying to change the format of the month that shows in the popup (not in the date that the picker actually I do not have any choice anywhere to do this, do I like to use a sub-string () or something else? What I normally display is Trying to change: Class = "ui-datepicker-title"> January & lt; / span & gt; ... & lt; / div & gt; Div>
Read more